Logic

[2.7.2] Boethius on Topical Logic

A. L. Komáromi1 Comment

The area of topical logic, – like many others – was founded by Aristotle in his work “Topics”, and continued by Cicero and Boethius, whose work exercised an enormous influence on medieval logic.
The aim of topical logic is to provide a practical heuristic method for finding credible, plausible (not necessarily true) arguments which can be used in situations where persuasion is needed, e.g. in a legal process. Boethius, in his book “On Topical Differentiae” presents topical arguments in a quasi-syllogistic structure, thus finding a good argument is identifying the middle term which links the extremes (see [1.3.9]).

The following OntoUML diagram presents the main concepts in the Topical Logic of Boethius (477-525 AD):

Boethius on topical logic
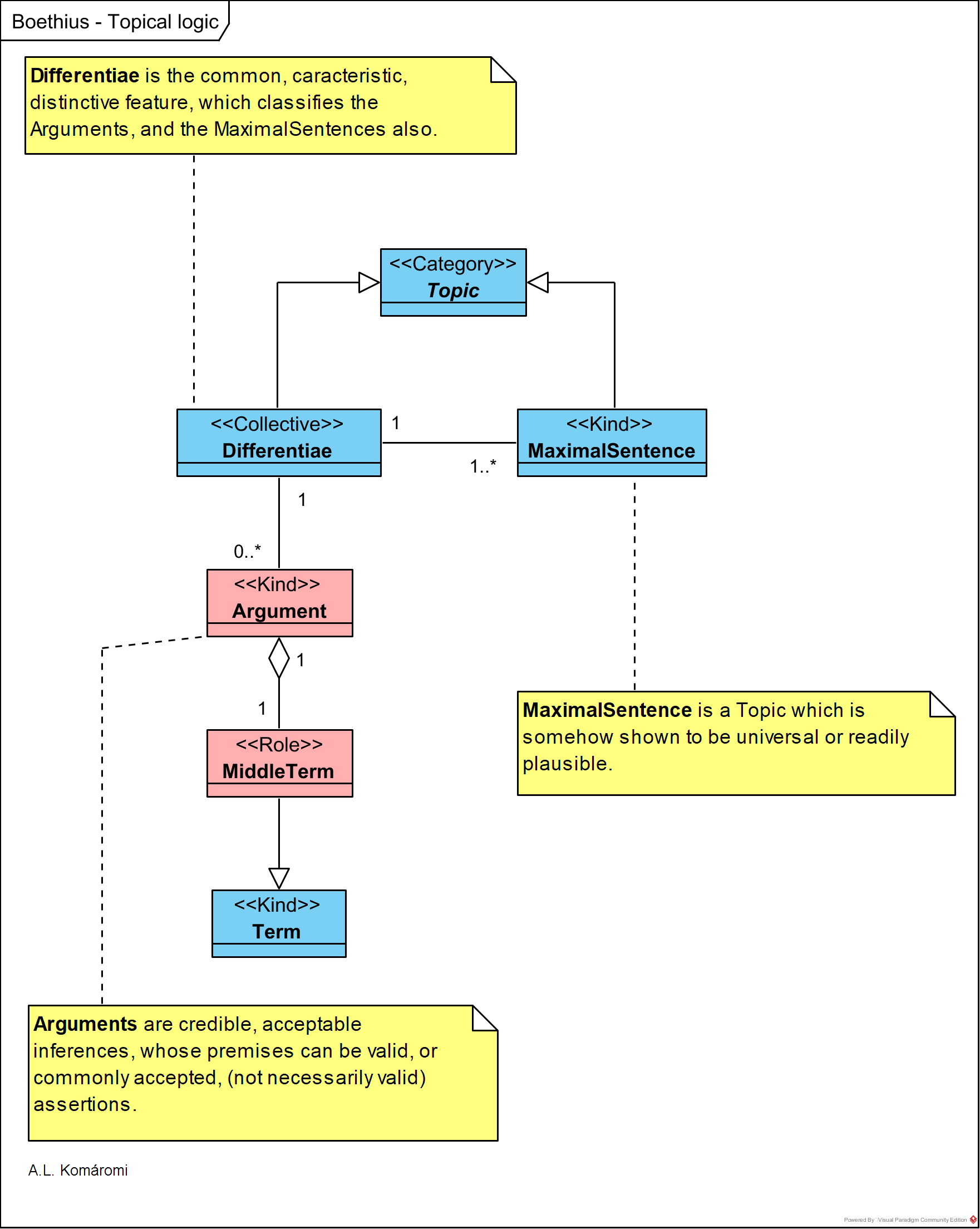
ClassDescription Relations
TopicTopic (locus) can be Differentiae and Maximal Sentences.
DifferentiaeTopical Differentiae are the common, caracteristic, distinctive feature, which classifies the Arguments, and the MaximalSentences also.
Boethius lists over 30 Differentiae, like:
– “from the lesser”
– “from an efficient cause”
– “definition”

A Differentiae is assotiated with at least one MaximalSentence; and with 0, 1 or many Arguments
MaximalSenteceMaximal Sentence (maxima propositio) is a Topic which is somehow shown to be universal or readily plausible. This way “will help to suggest exactly what sort of argument can be made using the differentia in question”, gives power to the Argument.
E.g. for the Differentiae “from an efficient cause” he lifts the following Maximal Sentences:
– “Those tings who have a natural efficient cause are themselves also natural.”
– “Where there is the cause, the effect cannot be ansent.”
– “Everything should be considered according to its causes.”
ArgumentArguments are credible, acceptable inferences, whose premises can be valid, or commonly accepted, (not necessarily valid) assertions (see [1.3.9]). Each Argument contains a MiddleTerm
MiddleTermSee in [1.3.9] also: The term shared by the premises is the Middle Term. MiddleTerm is are a role of a Term
TermSee in [1.3.9] also: Subjects and predicates of Arguments are Terms which can be either individual, e.g. Socrates, or universal, e.g. human. Subjects may be individual or universal, but predicates can only be universals.

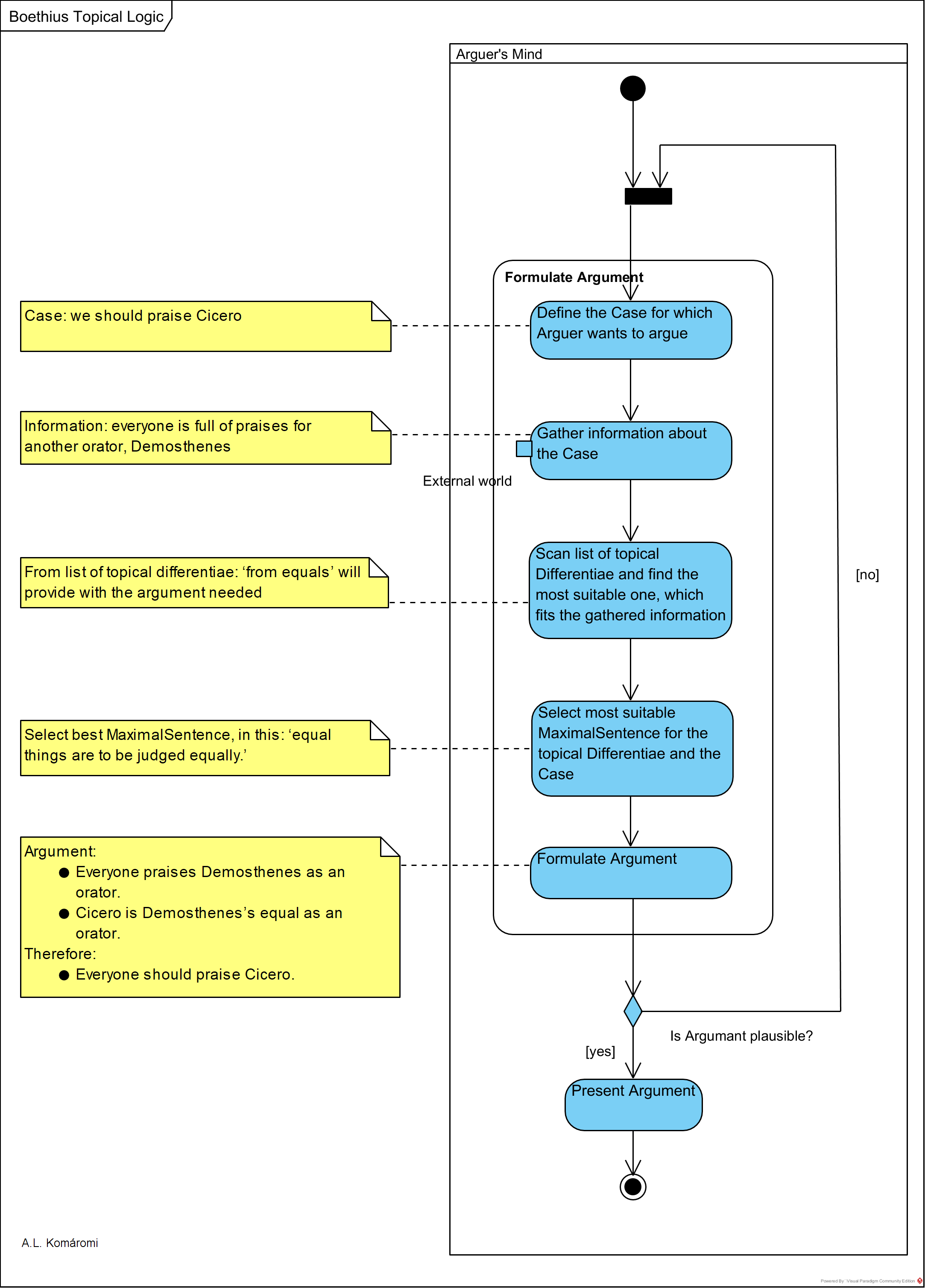
The UML activity diagram below shows the heuristic process of topical logic:

Boethius: heuristics of topical logic

Sources

  • All citations from: Marenbon, John, Boethius, Oxford University Press, 2003
  • Case presented in Activity Diagram from: Marenbon, John, “Anicius Manlius Severinus Boethius”, The Stanford Encyclopedia of Philosophy (Winter 2016 Edition), Edward N. Zalta

First published: 27/06/2019

[2.2.4] Ontological Structure of Stoic Logic

A. L. Komáromi8 Comments

Stoic logic, elaborated by Chrysippus (297-206 BC), is one of the two major systems of logic (the other one is Aristotelian logic) in the classical world and can be characterized by:

  • It is propositional logic (unlike the Aristotelian [1.3.9], which is term logic), because analyses the relations and truth values of assertibles (or propositions). Here logical variables are propositions, while in Aristotelian logic terms.
  • It is concerned more with particulars (unlike the Aristotelian logic, which is analyzing categorization and universals) reflecting thus the stoic view that only particulars are real existents (see also [2.2.5]).

The stoic logic, represented in the OntoUML diagram below, operates with the following main classes and relationships:

Stoic logic
ClassDescriptionRelations
SayableSayable (lekta) (see also in [2.2.2]): “are the underlying meanings in everything we say and think, but… also subsist independently of us. They are distinguished from spoken and written linguistic expressions: what we utter are those expressions, but what we say are the sayables.”
Assertible“Assertibles (axiômata) are sayables having a truth value: at any one time they are either true or false. So truth is temporal and assertibles may change their truth-value. They can never be true and false at the same time (law of non-contradiction) and they must be at least true or false (law of excluded middle).”subkind of Sayable
TruthValueThe truth value of an Assertible might change over time, so each value is valid from the startTime to endTime.characterizes Assertible
SimpleAssertibleSimple assertibles include propositions like: “it is cold”; “it is raining this morning” and “no one is running.” subkind ofAssertible; component of Non-simpleAssertible
Non-simpleAssertibleNon-simple assertibles are compound of simple assertibles linked with logical connectives, like: if.. than, and, either.. or, since, because. E.g. “if it is winter than it is cold”; “either it is day or night”; and “I am moving since I am working”.subkind of Assertible; is component of SimpleAssertible
PremisePremise is an Assertible, e.g. “it is winter”; “if it is winter than it is cold”.role of Assertrible; deducts conclusion
ConclusionConclusion is an Assertible, e.g. “it is cold”. role of Assertrible
ArgumentArguments relates two (or more) Premises to a Conclusion as cause and effect. At least one Premise has to be a Non-simpleAssertible. E.g.
Premise1: “if it is winter than it is cold”; if P than Q
Premise2: “it is winter”; P
Conclusion: “it is cold”; therefore Q		mediates between Premise and Conclusion; if Argument is valid can be reduced to StoicSyllogism
StoicSyllogismStoic syllogism “is best understood as a… natural-deduction system that consists of five kinds of axiomatic arguments (the indemonstrables) and four inference rules, called themata. An argument is a syllogism precisely if it either is an indemonstrable or can be reduced to one by means of the themata. Thus syllogisms are certain kinds of formally valid arguments. The Stoics explicitly acknowledged that there are valid arguments that are not syllogisms; but assumed that these could be somehow transformed into syllogisms.”
IndemonstrableThe five indemonstrables are:
1/ Modus ponens: If p, then q.  p. Therefore, q.
2/ Modus tollens: If p, then q. Not q. Therefore, not p.
3/ Not both p and q.  p. Therefore, not q.
4/ Modus tollendo ponens: Either p or q. Not p. Therefore, q.
5/ Modus ponendo tollens: Either p or q.  p. Therefore, not q.		member of StoicSyllogism
Themata“Complex syllogisms could be reduced to the indemonstrables through the use of four ground rules or themata. Of these four, only two have survived.
E.g. when from two assertibles a third follows, then from either of them together with the contradictory of the conclusion the contradictory of the other follows.”		member of StoicSyllogism

Sources

  • All citations from: Bobzien, Susanne, “Ancient Logic“, The Stanford Encyclopedia of Philosophy (Winter 2016 Edition), Edward N. Zalta (ed.)
  • Bobzien, Suzanne, Stoic Logic, Cambridge Companions Online © Cambridge University Press, 2006

First published: 13/6/2019
Updated: 15/1/2022